F2-1: Determination of the Internal Resistance of a Cell Using a Potentiometer

Apparatus

Leclanché Cell (filled to bottom of paint line with saturated Ammonium Chloride solution); metre bridge board; \(3\text{V}\) battery (fresh cells); jockey; switch; galvanometer with \(100\Omega\) series resistor; rheostat (\(\sim 15 \Omega\) resistance); resistors values: \(5\Omega\), \(10\Omega\), and \(20\Omega\); block with crocodile clips (for resistor); connecting leads (3 long, 7 short); 1 sheet graph paper.

F2-1.1

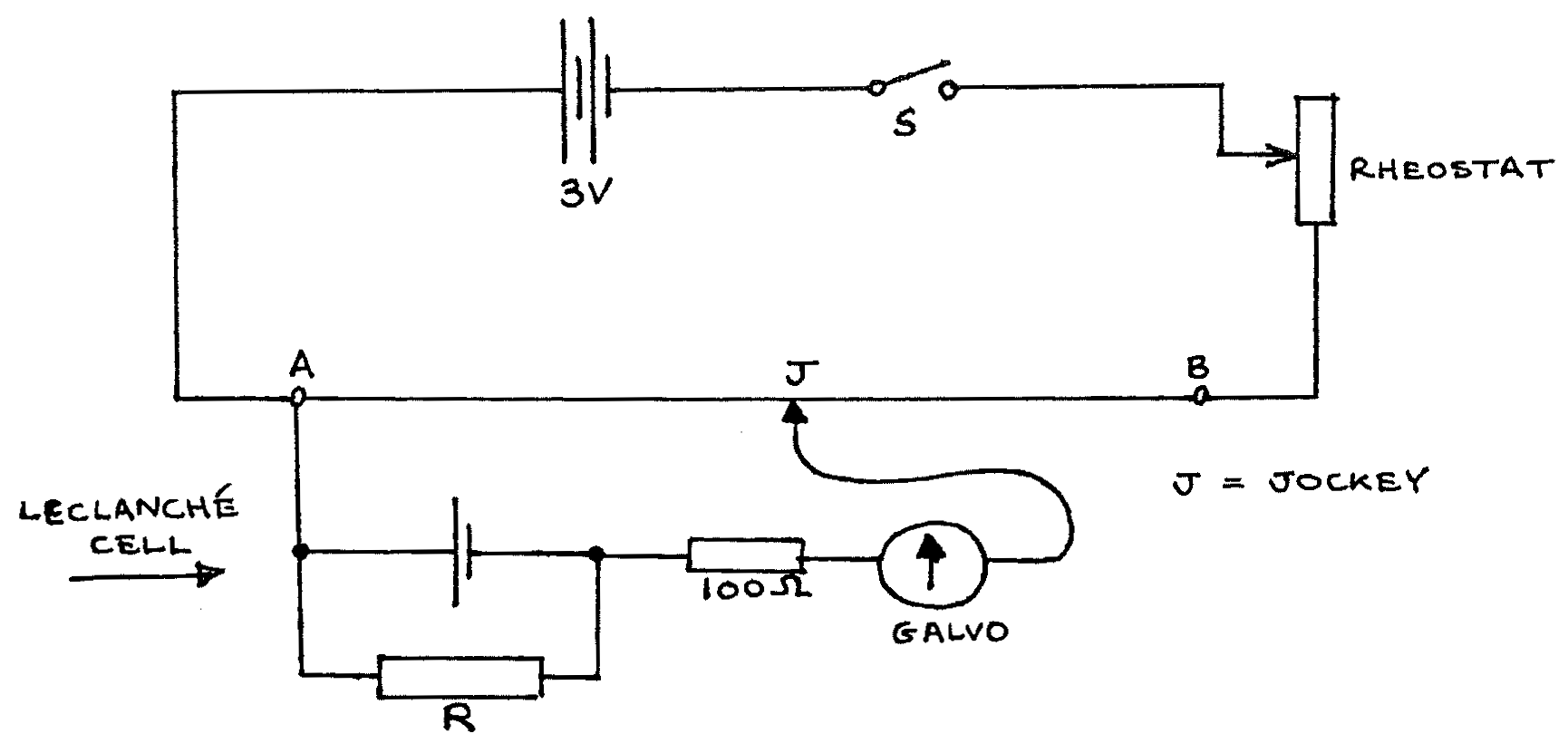
Procedure

  1. Construct the above circuit, with \(R =\infty\Omega\). Close the switch S. After placing J \(5\text{cm}\) from B, adjust the rheostat until the galvanometer reads zero (balance point). Note the length \(l_{\infty} = \overline{AJ}\). Open S.
  2. Connect \(R = 30\Omega\), Close S, and find the balance point. Read \(l = \overline{AJ}\). Repeat with \(R = 25, 20, 15, 10, \text{and } 5\Omega\). Tabulate \(R\) and \(l\). Open S.

NOTE: After the experiment, empty the Ammonium Sulphate solution out of the cell again, to ensure a maximum lifetime for the solution.

Theory

Consider the lower branch of the circuit when the galvanometer reads zero. It is effectively disconnected from the top branch of the circuit:

F2-1.2

\[\begin{split}I=\frac{E}{r+R}=\frac{V}{R}\\\end{split}\]

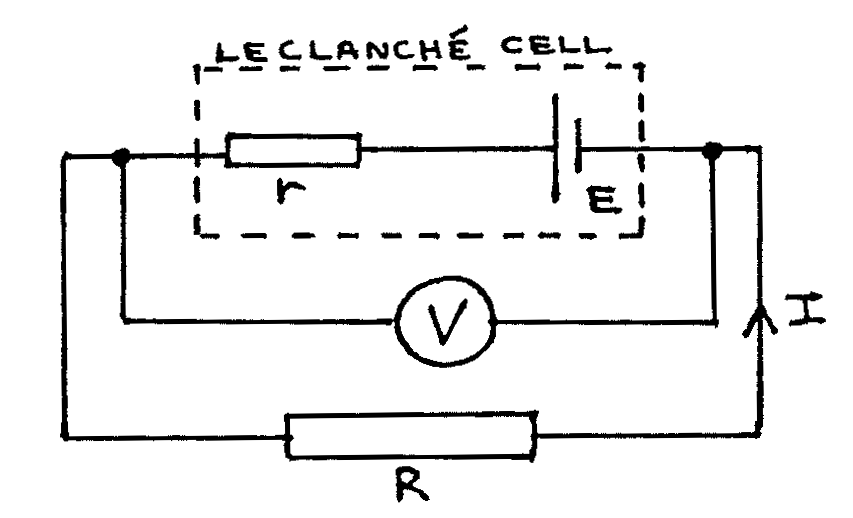
Therefore:

\[ER = Vr+VR\]

And therefore:

\[r = \frac{R(E-V)}{V}\]

However the length \(l\) is proportional to the potential difference \(V\), and when \(R=\infty\Omega\), \(V = E\). Thus let \(V = kl\) and \(E = kl_{\infty}\),where \(k\) is a constant. Therefore:

\[r = \frac{R(kl_{\infty}-kl)}{kl} = \frac{R(l_{\infty}-l)}{l}\]

And therefore:

\[\frac{1}{R} = \frac{l_{\infty}}{r} \left(\frac{1}{l} - \frac{1}{r}\right)\]

Analysis

  1. Plot a graph of \(\frac{1}{R}\) vs. \(\frac{1}{l}\) and find the gradient.
  2. Use the gradient, the value of \(l_{\infty}\), and the last equation in the theory only to find the internal resistance of the cell, \(r\).

Questions

    1. In the theory why can we say that the lower branch is ‘effectively disconnected’ from the top branch of the circuit?
    2. If the resistance of wire AB is \(2\Omega\) and its length is \(100\text{cm}\), find an expression for \(k\) in terms of \(V_{AB}\) only.
  2. Compare the Leclancé Cell and the modern Dry Cell. List a) the similarities and b) the differences.
  3. Define a) internal resistance and b) electromotive force. Thus explain carefully why in the theory, when \(R =\infty \Omega\), then \(V = E\).